Als meine Nichte vier Jahre alt geworden ist, fiel mir mal wieder auf, wie viel in dieser kurzen Zeit des letzten Jahres passiert ist. Kinder in diesem Alter entwickeln sich sehr schnell: Sie wachsen, erlernen neue lebenswichtige Fähigkeiten und Formen sozialer Interaktion. Sie altern. Mein Bruder, der Vater meiner Nichte, deren Onkel ich bin, ist in diesem einen Jahr sicherlich (aber nicht sichtlich!) auch gealtert. Selbstredend, dass einem erwachsenen Mann nicht die gleichen Entwicklungssprünge in der gleichen Zeit gelingen. Techniken wie das Bilden und Aussprechen komplexer Sätze und der sozialen Interaktion stellen für ihn keine Herausforderung mehr dar. Die Entwicklungen sind – im Vergleich zu einem Kleinkind – marginal. Hier allerdings beginnt die faszinierende Welt der Physik. Denn meine Nichte hat nicht nur größere Entwicklungssprünge in der gleichen Zeit hingelegt wie mein Bruder – sondern sie hat sogar noch weniger Zeit dafür gehabt.
Die Zeitdilatation ist eine komplizierte Angelegenheit. Besonders für solche, die sich nur noch dunkel an die allgemeine Relativitätstheorie aus dem Schulunterricht erinnern können. Zu solchen Leuten zähle ich auch mich selbst – doch ist meine Faszination für diese Phänomene ungebrochen und gerade die Zeitdilatation springt mir immer wieder in meinem armen Hirn herum. Wie nicht selten bei meinen Beiträgen im Bereich “Faszinationen” ist der folgende Beitrag allerdings mit Vorsicht zu genießen. Ich bin kein Physiker. Ich kann nicht garantieren, dass meine Berechnungen korrekt sind.
Viel mehr möchte ich mit meinem Beitrag die wunderbare Welt der Physik zeigen. Ihre Schönheit feiern, ihre Vielseitigkeit veranschaulichen und beweisen, dass jeder Spaß daran haben kann – ohne ein Experte zu sein. Die Physik ist schön und Du, verirrter Leser, bist es mit Sicherheit auch. Fangen wir also an.
Zeit
Im Alltag begegnet uns die Zeit als konstante Größe. Menschen, die in der gleichen Zeitzone leben, haben Uhren mit identischer Anzeige (sofern Sommer- und Winterzeit identisch ist) Dadurch wird der Eindruck erweckt, dass eine Sekunde immer eine Sekunde ist. Die Allgemeine Relativitätstheorie erklärt allerdings, dass dies nicht der Fall ist. Die Zeit, die für einen Körper vergeht, kann durch dessen Bewegung beeinflusst werden.
Ein sehr anschauliches Beispiel dafür, dass es keine absolute, sondern eine relative Zeit gibt, ist die Zeitdilatation durch Bewegung. Ein Versuchsaufbau sieht dazu wie folgt aus: In einem Flugzeug befinden sich zwei Parallel aufeinander gerichtete Spiegel. Zwischen diesen Spiegeln bewegt sich ein Photon, welches jeweils von einem Spiegel auf den gegenüberliegenden reflektiert wird und zurück. Das Photon bewegt sich dabei konstant mit Lichtgeschwindigkeit.

Wenn man aus der Perspektive des Flugzeugs das Photon betrachtet, so bewegt sich dieses Photon in der Tat nur von einer Spiegel-Fläche zur Gegenüberliegenden.

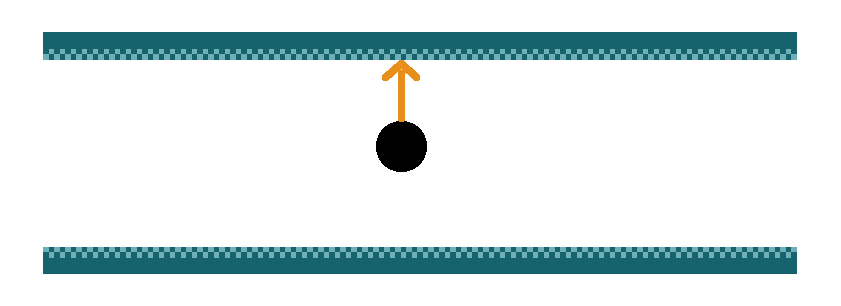

Die dafür benötigte Zeit definiert sich aus der Geschwindigkeit des Photons (Lichtgeschwindigkeit) und dem Abstand h zwischen beiden Spiegelflächen. Es ergibt sich die folgende Formel, die wir aus der Dynamik kennen: \[t = \frac{s}{v}\]

Es ist für die weitere Betrachtung nicht notwendig, ein konkretes h zu definieren. Behalten wir einfach im Kopf, dass aus der Perspektive des Flugzeugs die notwendige Zeit des Photons um von einem zum anderen Spiegel zu kommen wie folgt definiert ist:
\[t = \frac{h}{c}\]Interessant wird diese Betrachtung, sobald wir die Perspektive wechseln. Wie würde das Experiment für einen Beobachter aussehen, der nicht im Flugzeug ist, sondern sich auf dem Erdboden befindet?

Dadurch, dass wir das Experiment vom Erdboden aus betrachten, können wir eine neue relative Bewegung beschreiben. Während man vom Flugzeug aus lediglich die Bewegung des Photons zwischen den Spiegelflächen feststellen konnte, können wir nun zusätzlich auch die Bewegung des Flugzeuges an sich beobachten.
Beobachten wir nun den Weg, den das Photon zurücklegt, bemerken wir dass die zurückgelegte Strecke größer ist – und das im gleichen Beobachtungsintervall!


Tatsächlich lässt sich bei einer geraden und gradlinigen Bewegung des Flugzeuges über den Satz des Pythagoras ermitteln, wie viel größer der zurückgelegte Weg des Photons aus Sicht eines “ruhenden” Beobachters ist: Die zurückgelegte Strecke des Flugzeugs innerhalb der Zeit, die das Photon braucht um sich von einem Spiegel zum anderen zu bewegen und der Abstand zwischen den Spiegelflächen h spannt ein rechtwinkliges Dreieck auf. Der Weg des Photons stellt die Hypotenuse dar.
Sei a die zurückgelegte Strecke des Flugzeugs und h der Abstand zwischen den Spiegeln, dann lässt sich der Satz des Pythagoras wie folgt anwenden:
\[ s ^{2} = a ^{2} + h ^{2} \]
Wichtiger als die konkrete Ermittlung der entstehenden Differenz ist hier aber die Feststellung der variablen Größe. In der klassischen Physik wird davon ausgegangen, dass die Geschwindigkeit eines Körpers aus der zurückgelegten Strecke in einer bestimmten Zeit ermittelt wird. Es ist also die Geschwindigkeit variabel und abhängig von Zeit und Raum.
Bei der Betrachtung des Photons fällt aber auf, dass wir von einer konstanten Geschwindigkeit ausgehen, nämlich der Lichtgeschwindigkeit c. Demnach müssen die variablen Größen in diesem Beispiel nicht die Geschwindigkeit sein, sondern Raum und Zeit. Mit anderen Worten: Ein Meter ist nicht immer ein Meter und eine Sekunde nicht immer eine Sekunde. Genau dies wird mit der allgemeinen Relativitäts-Theorie beschrieben.
Der Versuchsaufbau mit den Spiegeln und dem Photon kann wie eine Uhr betrachtet werden. Hat der ruhende Beobachter neben sich eine identische Uhr stehen, so wird er feststellen, dass sein Photon häufiger an eine Spiegelfläche stößt als das Photon in der Uhr des Flugzeuges. Es vergeht also wirklich die Zeit des ruhenden schneller als die des sich bewegenden Körpers. Experimentell konnte man diese Abhängigkeit mit einer Atomuhr bereits nachweisen.
Raum
Das Verständnis dafür, dass sich durch Bewegung eine Zeitdilatation ergibt, ist grundlegend relevant, um die Zeitdilatation durch Gravitation zu verstehen. Denn Albert Einstein hat mit seiner allgemeinen Relativitätstheorie den Nachweis erbracht, dass Gravitation als Kraft nicht existiert.

Um diese erstaunlich und wenig intuitive Aussage zu erklären, hilft uns auch ein Gedankenexperiment weiter. Man stelle sich eine große Kiste vor, vielleicht in der Größe einer Fahrstuhlkabine. In dieser Kiste befinden sich verschiedene Objekte und ein menschlicher Beobachter. Steht diese Kiste auf dem Dach eines riesigen Hochhauses, wird dem Beobachter nichts ungewöhnlich vorkommen. (Sofern es für ihn nicht ungewöhnlich ist, sich innerhalb einer Kiste auf dem Dach eines riesigen Hochhauses aufzuhalten.) Die Objekte erscheinen ihm wie gewohnt ruhend und unter Einfluss der Gravitation.
Sobald allerdings ein Übeltäter käme und die Kiste vom Dach hebe und fallen ließe (oder ein Zauberer zauberte das Hochhaus weg) – mit anderen Worten: Sobald sich die Kiste im freien Fall befindet – wird der Beobachter folgendes feststellen: Die Objekte in der Kiste und auch er selbst scheinen schwerelos zu sein. Dadurch, dass die Gravitation für jedes Objekt in der Kiste als auch für den Beobachter und die Kiste selbst die gleiche Beschleunigung hervorruft, scheinen alle Objekte in Relation zum Beobachter in Ruhe und Schwerelos zu sein.
Albert Einstein hatte die Erkenntnis, dass es für einen Beobachter unmöglich ist, zu unterscheiden, ob sich die Kiste im freien Fall befindet oder im Weltraum. Mehr noch: Die Kiste im freien Fall verhält sich nicht nur ähnlich zu einer Kiste im Weltall – sondern die wirkenden Kräfte sind exakt identisch.

Woran liegt das? Einstein erklärt dieses Phänomen mit der Raumzeit. Alle Objekte im Universum bewegen sich seiner Erklärung nach auf geraden Bahnen in gleichförmiger Geschwindigkeit. Die Bahnen allerdings, auf die wir uns permanent mit gleichförmiger Geschwindigkeit bewegen, befinden sich in einer Raumzeit, die beispielsweise durch Masse gekrümmt wird.
Befindet sich ein Beobachter im freien Fall, so registriert er eine Beschleunigung, weil die Krümmung der Raumzeit in Richtung des Erdkerns, also des Massepunktes, zunimmt. Es wirkt dabei keine physikalische Kraft, sondern vielmehr handelt es sich um eine geometrische Eigenschaft der Raumzeit. Kann die Geometrie wirklich einen so fundamentalen Einfluss auf die Wahrnehmung haben? Am folgenden Beispiel wird es vielleicht klar:
Aus der Geometrie des Schulunterrichts wissen wir, dass zwei parallele Geraden einander nie schneiden. Sie verlaufen auf der Fläche unendlich lang parallel. Auf einer Kugeloberfläche sieht das allerdings bereits anders aus. Betrachten wir zwei Rennautos, die am Äquator einer Miniatur-Erde ein Rennen in Richtung Norden fahren und dabei exakt parallel starten, so werden wir sehen, dass diese Autos, obwohl sie parallel starten und immer geradeaus fahren einander immer näher kommen, bis sie einen der Pole erreicht haben.
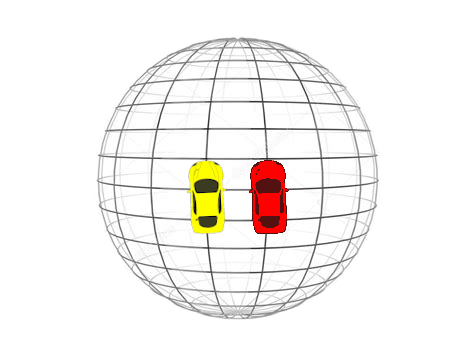
Zwischen den beiden Autos herrscht aber keine Kraft, die sie aneinander drückt, wenn sie zu einem Pol fahren oder sie auseinandertreibt, wenn sie sich von einem Pol in Richtung Äquator wieder voneinander entfernen. Diese Bewegung wird nicht durch das Wirken physikalischer Kräfte sondern durch die simple Geometrie des Raumes hervorgerufen. So verhält es sich auch mit der Raumzeit.

Deine Füße sind jünger als dein Kopf
Aus den gelernten Grundsätzen zu Zeit und Raum kann man nun Schlussfolgerungen ziehen. Wir wissen nun, dass bewegte Objekte langsamer altern als ruhende Objekte. Daraus resultiert auch, dass Objekte mit hoher Geschwindigkeit langsamer altern als Objekte mit geringer Geschwindigkeit. Außerdem haben wir gelernt, dass die Gravitation selbst ein Zustand ständiger Bewegung ist. Aufgrund der von Masse gekrümmten Raumzeit bewegen sich Objekte in der Nähe des Massepunkts schneller als Objekte, die weiter davon entfernt sind.
Das sind keine theoretischen Erkenntnisse, sondern Phänomene, die man in der realen Welt beobachten und Messen kann. Ein gutes Beispiel hierfür ist das Vorkommen von Myonen auf der Erdoberfläche. Myonen sind Quanten-Teilchen, die mit hoher Geschwindigkeit durchs All rasen. Sobald sie in die Atmosphäre der Erde gelangen, beginnen sie zu zerfallen. Die Zeit, die ein Myon braucht, um zu zerfallen, ist geringer als die Zeit, die es braucht, um die Erdoberfläche zu erreichen. Dennoch kann man sie fast überall messen. Woran liegt das?
Die Myonen bewegen sich schnell. Sehr schnell. Schnell genug, dass ihr eigenes Altern relativ zur Erde viel weniger schnell voranschreitet. Während für den ruhenden Beobachter auf der Erde eine Myonen-Lebensdauer vergeht, ist für das Myon selbst, also das bewegte Objekt, nur ein Bruchteil davon vergangen. (Außerdem treten noch Effekte wie die Längenkontraktion auf, die ich vielleicht später in einem anderen Beitrag mal thematisieren werde.) Dass Myonen auf der Erdoberfläche messbar sind, ist ein Beweis für die Zeitdilatation und die Korrektheit der theoretischen Berechnungen.
Man kann also mit Fug und Recht behaupten: Deine Füße sind jünger als dein Kopf. Und: Kleine Menschen altern langsamer als große Menschen. Diese Erkenntnisse bringen uns nun zurück zu meiner kleinen Nichte, die zum Altern weniger Zeit hatte als ihr Vater, der mein Bruder ist.
Bruchteile von Sekunden
So viel zum allgemeinen Verständnis der Raumzeit und der Zeitdilatation. Nun wollen wir doch mal einen Taschenrechner rausholen und uns von den Socken hauen lassen! Leider – so viel sei zuvor gesagt – müssen wir ein paar Abstriche machen, was die Genauigkeit der folgenden Berechnungen angeht. Es wird vielmehr eine Größenordnung aus ihr hervorgehen als eine tatsächliche Größe. Das ist eines dieser Praktiken, zu denen Physiker gerne neigen, wenn es um SEHR GROßE oder sehr kleine Sachen geht.

Beginnen wir damit, die Unterschiedlichen Einflüsse der Gravitation auf meine Nichte und meinen Bruder zu definieren. Meine Nichte ist vom 3. bis zum 4. Geburtstag etwa 4cm gewachsen. Von 90cm auf 94cm. Deshalb nehmen wir für den Zeitraum von einem Jahr (relativ zum Erdmittelpunkt) ihre Größe mit 0,92m an. Mein Bruder, ihr Vater, ist in dem Zeitraum nicht gewachsen und seine Größe kann mit 1,785m definiert werden.
Außerdem brauchen wir zum Ermitteln der Zeitdifferenz den Abstand der beiden Objekte zum Erdmittelpunkt. Wir gehen davon aus, dass sich Vater und Tochter primär am Erdboden aufhalten und verwenden zudem den mittleren Erdradius von 6.371.000 m
Daraus ergeben sich die folgenden zwei Größen:
\[R_{tochter} = 6371000,92m\]
\[R_{vater}=6371001,785m\]
R ist dabei die Entfernung zum Erdmittelpunkt. Mit diesen Daten können wir nun die Zeitdifferenz der Koordinatenzeiten von Vater und Tochter ermitteln.
\[\Delta T = \frac{T}{\sqrt{1-\frac{2\cdot G \cdot M}{c^{2} \cdot R_{vater}}}}-\frac{T}{\sqrt{1-\frac{2\cdot G \cdot M}{c^{2} \cdot R_{tochter}}}}\]In dieser Gleichung befinden sich zudem noch verschiedene Konstanten die wie folgt angenommen werden können:
G – Gravitationskonstante
\[G = 6,67430 \cdot 10^{-11} \frac{m^{3} \cdot kg}{s^{2}}\]
M – Erdmasse
\[M = 5,9722 \cdot 10^{24} kg\]c- Lichtgeschwindigkeit
\[c = 299792458 \frac{m }{s}\]T – Die Zeit, die wir untersuchen wollen. Diese definieren wir auf ein siderisches Vaterjahr
\[ T = 365d+6h+9min+9,54 s = 31558149,54s \]Setzen wir die ermittelten Werte und die Konstanten in die oben angegebene Formel ein, ergibt sich folgende Gleichung:
\[\Delta T = \frac{31558149,54s}{\sqrt{1-\frac{2\cdot 6,67430 \cdot 10^{-11} \frac{m^{3} \cdot kg}{s^{2}} \cdot 5,9722 \cdot 10^{24} kg}{(299792458 \frac{m }{s})^{2} \cdot 6371001,785m}}}-\frac{31558149,54s}{\sqrt{1-\frac{2\cdot 6,67430 \cdot 10^{-11} \frac{m^{3} \cdot kg}{s^{2}} \cdot 5,9722 \cdot 10^{24} kg}{(299792458 \frac{m }{s})^{2} \cdot 6371000,92m}}}\]Zugegeben, ein ziemlicher Klopper. Dennoch kein Grund, sich davor zu fürchten. Das Ergebnis liefert schließlich ein Taschenrechner. Mit vor Aufregung zitternden Fingern öffnete ich also den guten alten Desmos Web Taschenrechner, der mir schon in manch kniffliger Stunde geholfen hat und tippte präzise die Daten ein:

NULL! Was für eine Beleidigung! Scheinbar habe ich die Rundungsgrenze des Taschenrechners überwunden. Soll wirklich schon nach 9 oder 10 Nachkommastellen Schluss sein? Nein! Das kann ich nicht auf mir sitzen lassen. Geogebra muss her!

Heureka! Das nenne ich mal ein phänomenales Ergebnis!
\[\Delta T = \frac{0,0000000037253}{0,999999996077}s \approx 0,0000000037253s\]Mit anderen Worten: Das Jahr meiner Nichte war ganze 0,00000000372530001 Sekunden kürzer als das Jahr meines Brudes das sind 3,72530001 Nanosekunden! – die erstaunlichen Entwicklungen geschahen also in einer noch viel kürzeren Zeit als gedacht und sind deshalb umso erstaunlicher!
Knick in der Stoppuhr
Allerdings warne ich noch vor eventuellen Rundungsfehlern. Wir haben eine ganze Reihe von Vereinfachungen vorgenommen und den ein oder anderen sprichwörtlichen Knick im Zollstock (oder eher Knick in der Stoppuhr) zugelassen. Vermutlich sind es nicht exakt 3,7253 Nanosekunden, die die Zeit meiner Nichte von der Zeit meines Brudes trennen.
Außerdem haben wir, wenn wir im Bereich der Relativitäts-Theorie bleiben wollen, auch nicht die Längenkontraktion berücksichtigt, die beim rapiden Wachsen meiner Nichte mit einer unfassbaren Geschwindigkeit von 4cm/jahr (oder: 0,00000000000000035208 km/h) auftreten. Auch deshalb ist das Ergebnis mit Vorsicht zu genießen.
Und dennoch: Meine Nichte altert langsamer, solang sie kleiner und näher am Erdkern ist als mein Bruder – und wer etwas gegen das Altern tun will, der kann damit anfangen, dass er sich auf den Boden legt oder Urlaub am Toten Meer macht.

